Linear Programming (LP) หรือที่ภาษาไทยเรียกว่า การโปรแกรมเชิงเส้น คือการเทคนิคที่ใช้ในการแก้ปัญหาการจัดสรรทรัพยากรที่มีอยู่อย่างจำกัด เพื่อให้ได้ผลลัพธ์ที่ดีที่สุด ซึ่งอาจจะหมายถึง กำไรสูงสุด หรือ ต้นทุนต่ำที่สุดเป็นต้น
เทคนิค Linear Programming นี้ถูกนำมาใช้เพื่อช่วยในการตัดสินใจทางธุรกิจ เช่น ปัญหาในการวางแผนการตลาด ปัญหาในการจัดสรรเงินลงทุน หรือ ปัญหาการผลิตในโรงงานหรืออุตสาหกรรม เป็นต้น
เทคนิค Linear Programming จะนำมาใช้เพื่อหาคำตอบที่ดีที่สุดของฟังก์ชันเชิงเส้น (Linear Function) ซึ่งสามารถเขียนในรูปแบบคณิตศาสตร์ได้ดังนี้
f = C1X1 + C2X2 + ... + CnXn
เพื่อให้เห็นภาพมากขึ้น มาดูตัวอย่างปัญหาจากตัวอย่างข้างล่างกันดีกว่า
บริษัทเฟอร์นิเจอร์แห่งหนึ่งมีผลิตภัณฑ์ที่ผลิตคือ โต๊ะและเก้าอี้ โดยมีทรัพยากรหลักที่ใช้ในการผลิตโต๊ะและเก้าอี้คือ ช่างไม้และไม้ ซึ่งทางผู้จัดการกำหนดมาว่าในรอบการผลิตถัดไปทางบริษัทมีช่างไม้ว่างสำหรับการทำงานทั้งหมด 1,250 ชม และบริษัทมีไม้ที่พร้อมใช้งานทั้งหมด 3,600 แผ่น จากประสบการณ์ที่ผ่านมาบริษัทรู้ว่าการสร้างเก้าอี้หนึ่งตัวจะใช้เวลาของช่างไม้ 4 ชม และใช้ไม้ 9 แผ่น ส่วนการสร้างโต๊ะหนึ่งตัว จะใช้เวลาของช่างไม้ 6 ชม และใช้ไม้ 36 แผ่น บริษัทขายเก้าอี้ที่ตัวละ 420 บาท และ ขายโต๊ะตัวละ 700 บาท บริษัทต้องการรู้ว่าควรจะผลิตโต๊ะและเก้าอี้อย่างละกี่ตัวเพื่อจะทำรายได้ให้มากที่สุดจากทรัพยากรที่มีอยู่
จากที่เราเคยเรียนหนังสือกันมา เราก็จะใช้วิธีการวาดกราฟ ตีเส้นแล้วหาจุดตัด จากนั้นคำนวณหาว่าจุดตัดกราฟไหนที่จะให้ค่าที่ดีที่สุด แต่ในบทความนี้เราจะมาใช้ Microsoft Excel ช่วยเราแก้ปัญหา Linear Programming กัน
เริ่มต้นด้วยการเตรียม Excel ของเราให้พร้อมกันก่อน ในการแก้ปัญหา Linear Programming ด้วย Microsoft Excel เราจะต้องมี Add-in ที่ชื่อว่า Solver ซึ่งเราสามารถติดตั้งได้ฟรี ดูวิธีการติดตั้ง Solver Add-in ที่นี่
เมื่อทำการติดตั้ง Solver Add-in เรียบร้อยแล้วก็มาสร้าง Linear Programming model กันบน excel เลยดีกว่า โดยการสร้าง Linear Programming Model นั้นจะมีองค์ประกอบสำคัญอยู่ 3 อย่าง คือ
- การกำหนดตัวแปรที่ถูกต้อง โดยตัวแปรมักจะเป็นจำนวนของสิ่งที่เราต้องการทราบว่าต้องมีเท่าไหร่จึงจะทำให้ Objective function ได้ผลลัพธ์ที่เราต้องการหรือดีที่สุด
- การกำหนดสูตรของเป้าหมายที่เราต้องการให้ได้ผลลัพธ์ที่ดีที่สุด (Objective function)
- การกำหนดเงื่อนไขข้อจำกัด (constraints) ที่ถูกต้องและครบถ้วน
คราวนี้เรามาลองสร้างโมเดลจากตัวอย่างบริษัทเฟอร์นิเจอร์ข้างต้นกันโดยเริ่มจากการกำหนดตัวแปร ในกรณีนี้ เราต้องการหาจำนวนโต๊ะและเก้าอี้ที่เราควรจะผลิตเพื่อให้ได้รายได้สูงสุด ดังนั้นเราจะกำหนดตัวแปรเป็นโต๊ะและเก้าอี้ดังรูปข้างล่าง

จากตาราง Excel ข้างต้น เราใส่ค่าเริ่มต้นให้จำนวนเก้าอี้กับโต๊ะเป็น 1 ซึ่งค่าเริ่มต้นนี้เราจะใส่เป็นอะไรก็ได้เพราะสุดท้ายแล้วค่านี้จะถูกคำนวณโดย Solver เพื่อให้ได้ค่าที่ดีที่สุดในภายหลัง นอกจากนี้จะเห็นได้ว่าเราได้ใส่รหัสสี (color code) ของจำนวนเก้าอี้และโต๊ะให้เป็นสีเขียวเพื่อบอกให้เรารู้ว่ามันเป็นตัวแปรที่สามารถปรับเปลี่ยนได้เพื่อให้ได้คำตอบที่ดีที่สุด ส่วนแถวที่สามเราใส่ราคาขายต่อหน่วยของเก้าอี้และโต๊ะตามที่โจทย์กำหนดให้ ซึ่งค่านี้จะถูกนำมาใช้ในการคำนวณหา Objective function ดังรูปข้างล่าง
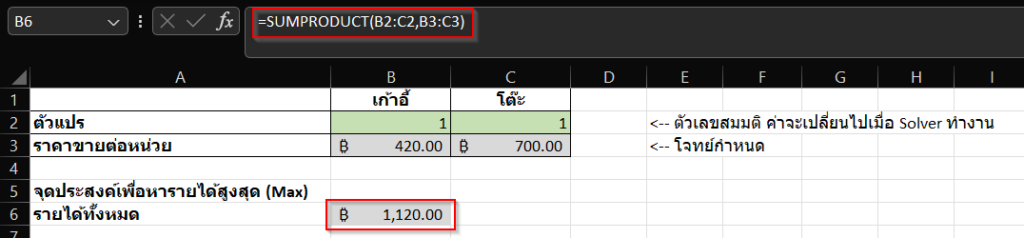
เรารู้ว่ารายได้ทั้งหมดเกิดจากผลลัพธ์ของการคำนวณตามด้านล่างนี้
รายได้ทั้งหมด = (จำนวนเก้าอี้ x ราคาเก้าอี้ต่อหน่วย) + (จำนวนโต๊ะ x ราคาโต๊ะต่อหน่วย)
ดังนั้นเราสามารถใช้ฟังก์ชัน SUMPRODUCT เพื่อช่วยในการคำนวณได้ โดยใส่สูตรในช่อง B6 ให้เป็น =SUMPRODUCT(B2:C2,B3:C3) ซึ่งจะทำให้ได้รายได้ทั้งหมดคำนวณออกมาขึ้นกับจำนวนเก้าอี้และโต๊ะที่เราใส่ไว้ ซึ่งในกรณีนี้เราใส่ค่าเก้าอี้และโต๊ะเป็น 1 ดังนั้นจะได้รายได้เป็น (420 x 1) + (700 x 1) = 1,120
ถึงตอนนี้เราได้ทำกำหนดตัวแปรและ objective function แล้ว ส่วนสุดท้ายที่เหลืออยู่คือการกำหนดเงื่อนไขข้อจำกัดทั้งหมดลงในโมเดลของเรา ซึ่งเราสามารถกำหนดได้ตามรูปข้างล่าง
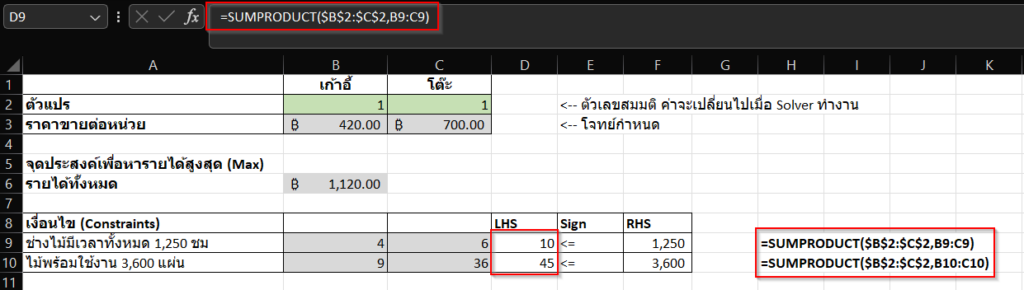
การกำหนดเงื่อนไขจะเริ่มด้วยการเขียนเงื่อนไขที่โจทย์กำหนดมาให้ก่อนซึ่งในตารางข้างบนเราเขียนออกมาได้ทั้งหมดสองเงื่อนไขใน Cell ที่ A9 และ A10 ในแถวที่ 9 เราจะกำหนดเงื่อนไขข้อจำกัดเรื่องจำนวนชั่วโมงทำงานของช่างไม้ ซึ่งจากโจทย์เรารู้ว่าช่างไม้ต้องใช้เวลา 4 ชม และ 6 ชม ในการสร้างเก้าอี้และโต๊ะหนึ่งตัวตามลำดับ
ในตารางข้างบนจะเห็นว่าเรามีการกำหนด LHS, Sign, RHS ซึ่งเป็นการระบุเงื่อนไขของสมการเส้นตรง โดยเราต้องทำสมการให้อยู่ในรูปของสมการเส้นตรง
C1X + C2X2 + ... + CnXn = A
- LHS คือ Left Hand Side หมายถึงสูตรทางฝั่งซ้ายของสมการ
- Sign คือ เครื่องหมายของสมการนี้
- RHS คือ Right Hand Side หมายถึงตัวเลขทางฝั่งขวาของสมการ
ดังนั้นเราจะใส่สูตร =SUMPRODUCT($B$2:$C$2,B9:C9) ไว้ที่ Cell D9 และ =SUMPRODUCT($B$2:$C$2,B10:C10) ไว้ที่ Cell D10 จากนั้นให้ใส่ค่า 1,250 และ 3,600 ที่ Cell F9 และ F10 ตามลำดับ
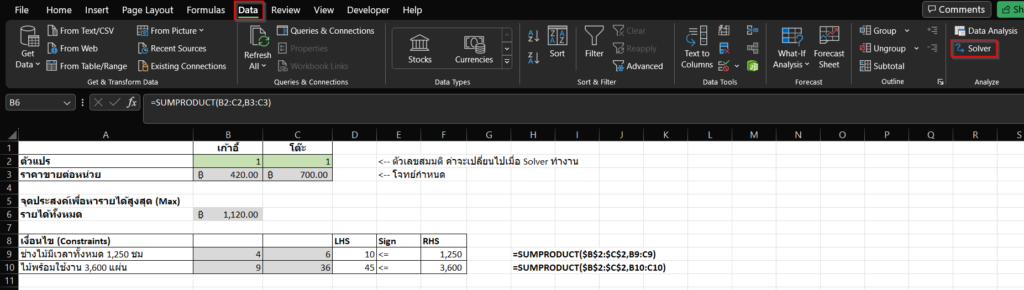
ถึงตอนนี้เราก็ได้กำหนดองค์ประกอบทั้งหมดของโมเดลเราครบสามอย่างแล้ว คราวนี้เราก็จะมาใช้งาน Solver เพื่อช่วยเราหาจำนวนเก้าอี้และโต๊ะที่เราควรจะผลิตเพื่อให้ได้รายได้สูงที่สุดกัน โดยให้เราเลือกไปที่ Cell B6 แล้วกดที่เมนู Data->Solver
หลังเลือก Solver จะมีหน้าต่าง Solver Parameters ขึ้นมาให้เราใส่ข้อมูล ถ้าเราเลือก Cell B6 ไว้ก่อนเลือกเมนู Solver ค่า $B$6 จะถูกเลือกเป็น Objective โดยอัตโนมัติ จากนั้นเราต้องกำหนดค่าต่างๆที่วงไว้ให้ถูกต้าง
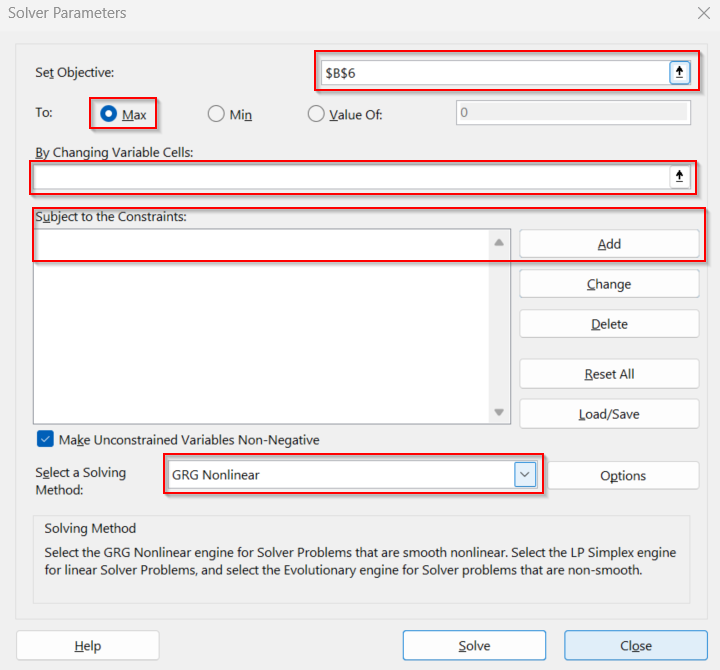
เนื่องจากปัญหานี้เป็นการหาค่าสูงสุดเราจึงเลือก Max จากนั้นให้เราเลือก variable cells และ constraints ให้ถูกต้อง และกำหนด Solving method เป็น Simplex LP ดังนั้นหลังจากกำหนด Parameters เสร็จ จะมีหน้าตาดังนี้
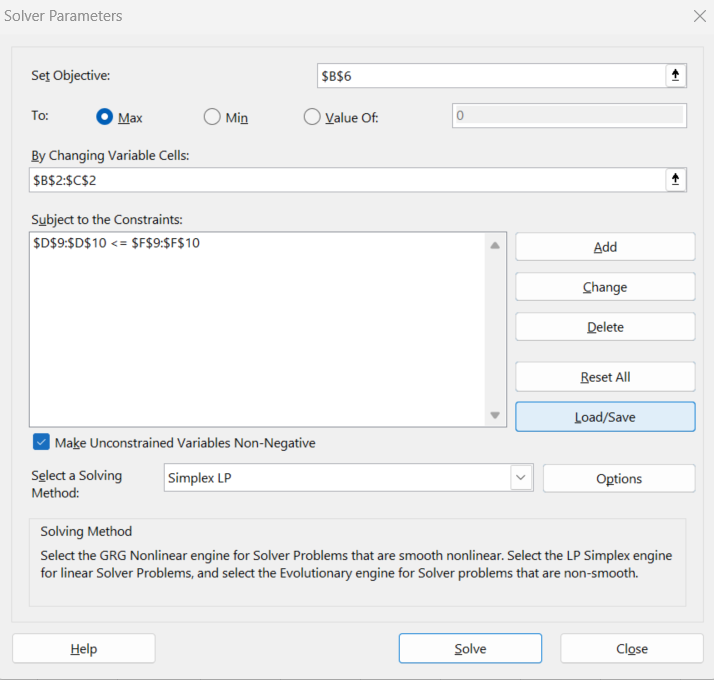
เมื่อกำหนด parameters เรียบร้อยแล้วให้กดที่ปุ่ม Solve หาก Solver ค้นพบคำตอบให้เราเลือก Keep Solver Solution แล้วกด OK ซึ่งมันจะแสดงผลลัพธ์มาบนตารางของเราดังแสดงข้างล่าง
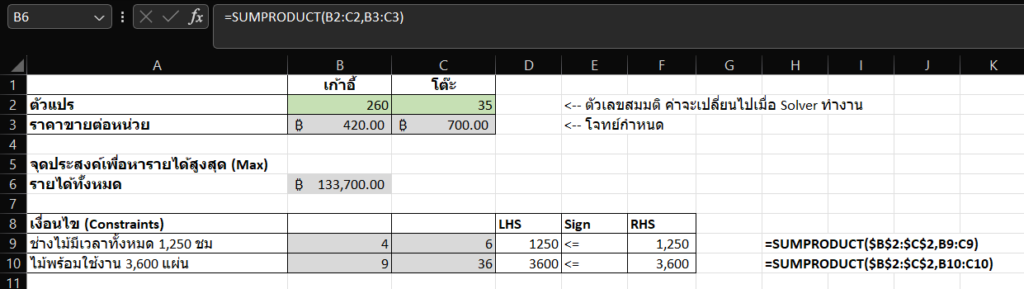
ดังนั้นจะทำให้เราได้คำตอบจากปัญหาว่าเราควรจะต้องผลิตเก้าอี้ 260 ตัว และผลิตโต๊ะ 35 ตัว ซึ่งจะทำให้ขายได้รายได้ทั้งหมด 133,700 บาท
เพียงเท่านี้เราก็สามารถแก้ปัญหา Linear Programming ได้แล้ว ความยากของการทำคือการกำหนดตัวแปรและสร้างโมเดลที่ถูกต้องให้ได้ เราควรกำหนด Format และใส่ Color code เพื่อช่วยให้เราทำงานได้ง่ายขึ้นด้วย